摘要

本文我们通过调整光波导长度的整数配比和整数破缺配比来研究了电磁波(EM wave)在一维PT对称双联通三角形光波导网络(one-dimensional PT-symmetric two-segment-connected triangular optical waveguide Network，简称1D PTSTSCTOWN)的奇异传输特性。研究发现：在这种PT对称的光学系统中，在光波导长度为整数配比的系统中，在其极值破缺点附近，EM wave最大能产生超强奇异透反射率。在光波导长度为整数破缺配比的系统中，在其极值破缺点附近，EM wave能产生的超强奇异透反射率。此外，光波导长度由整数到整数破缺配比的过程中，反射谱会出现较大的变化，由没有反射谷到产生反射深谷。这意味着波导长度为整数配比的系统没有不可见特性，而波导长度为整数破缺配比的系统不仅能产生不可见特性，而且能产生双向不可见特性，这加深了人们对PT对称光波导网络的认识。

1D PTSTSCTOWN模型

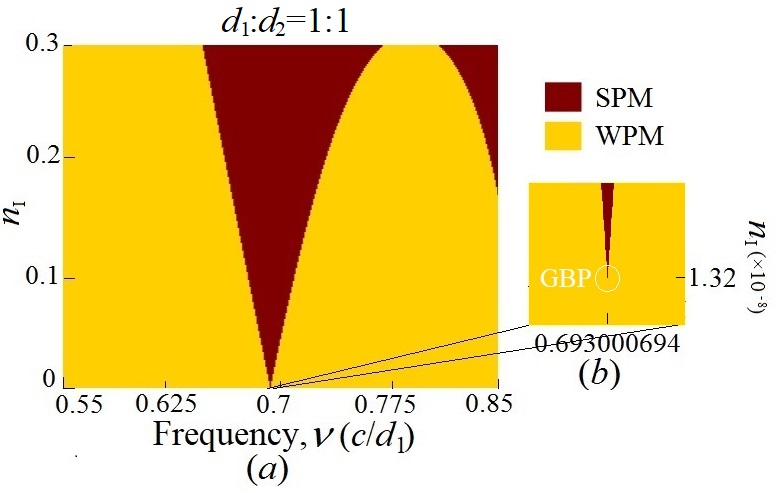
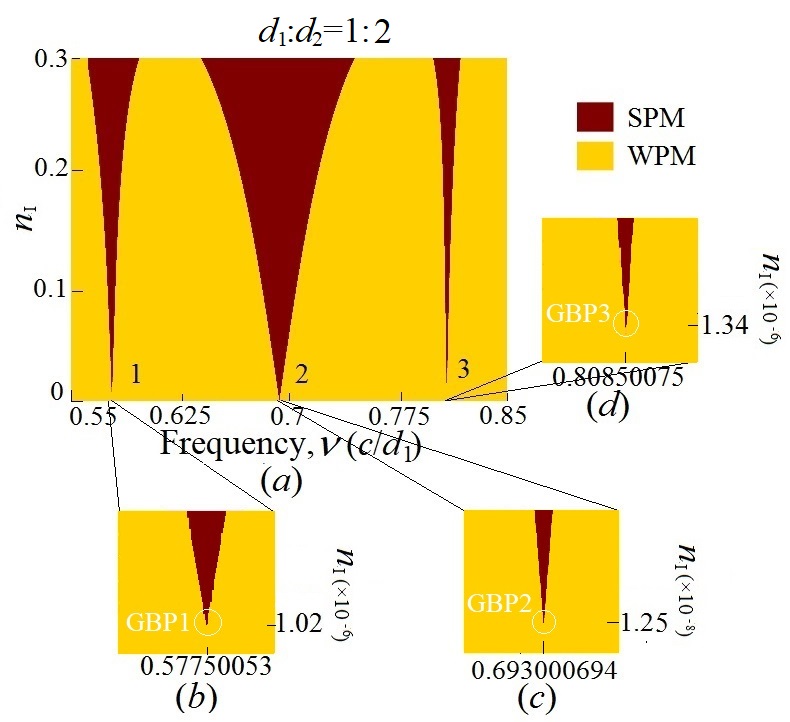
本文设计的1D PTSTSCTOWN的周期网络模型如下图所示，该网络由三个元胞、一个入口和一个出口组成。其中，每一个元胞相邻的连个节点由两段长度分别为$d_1$和$d_2$的PT对称光波导连接，长度配比$d_1:d_2=1:t$。PT对称光波导由三段长度相同、折射率呈对称分布的二氧化硅光波导组成。在下一节，我们研究了$t=1,2$作为整数配比例子的PTSTSCTOWN，以及$t=1-10^{-8},2-10^{-8}$作为整数破缺配比例子的PTSTSCTOWN的折射率与反射率。

PT对称极值破缺点

从广义布洛赫定理$\psi_K(N+T)=\psi_K(N)e^{iK·T}$可知：当EM波在具有拓扑平移周期性的光波导网络传播时，第$N+T$个原胞的波函数与第$N$个原胞的波函数相差一个$e^{iK·T}$因子。当$K$为实数的时候，$KT$也为实数，此时EM在网络中传播只会发生$e^{iK·T}$相位变化，振幅始终保持不变，这种光子模式称为正常传播模式(OPM)。当$K$为复数$K_a+iK_b$时，EM在网络中传播不仅会发生$e^{iK_a·T}$相位变化，振幅也会发生$e^{-K_b·T}$，且$K_b>0$时，振幅是衰减的，而$K_b>0$时，振幅是增益的，这两种光子模式分别被称为衰减模式(APM)和增益模式(GPM)，均属于非正常传播模式。
光子模式的分布需要由网络的色散关系$cos(K)=f(v)$来确定，当$|f(v)|\le1$时，布洛赫波矢$K$具有实数解，所以该频率的EM在网络中以OPM传播，而$|f(v)|>1$时，布洛赫波矢$K$为复数解，且由于真空和/或普通材料组成的光波导网络只存在衰减机制，所以EM以APM传播。由此可以判断出：在真空和/或普通材料组成的一维三角形三材料光波导网络中，$|f(v)|=1$是光子传播模式的分界点。
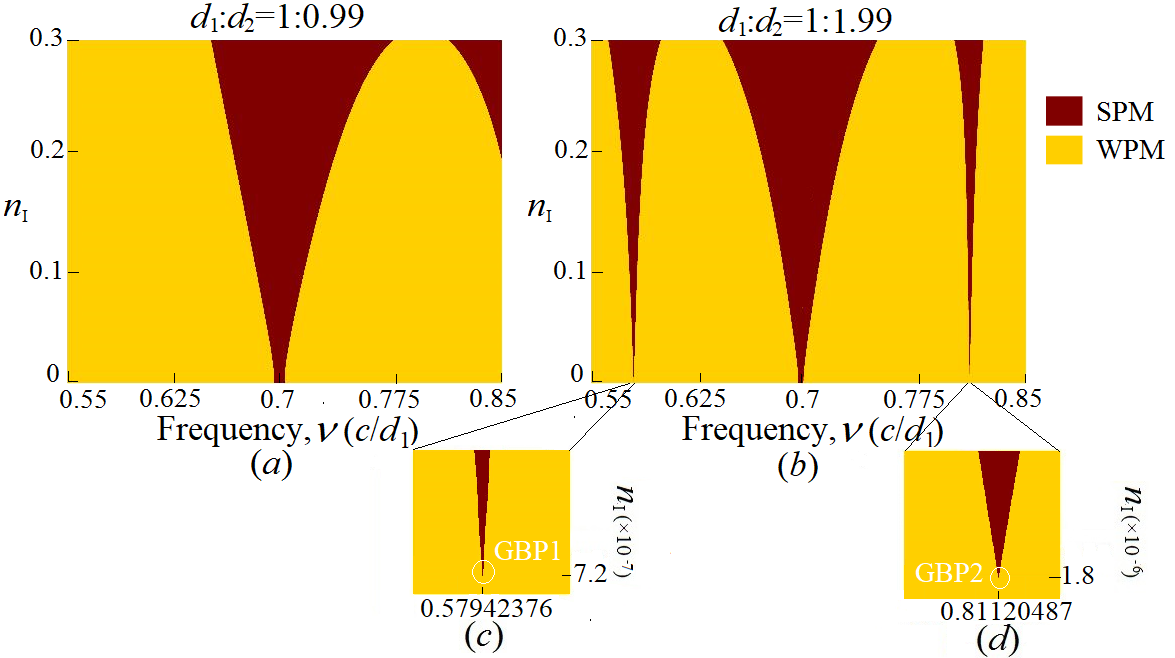
$|f(v)|=1$可以作为PT对称光波导网络的光子模式分界点，并且将$|f(v)|\le1$对应的布洛赫波矢$K$确定的波导网络产生的光子模式定义为弱模式(Weak Propagation Mode)，简称WPM；将$|f(v)|>1$对应的布洛赫波矢K 确定的波导网络产生的光子模式定义为强模式(Strong Propagation Mode)，简称SPM。而自发破缺点则是WPM和SPM交界处材料的折射率虚部$n_I$的值。一般而言，在自发破缺点处，即两种模式(WPM与SPM)的交界处，系统会产生奇异的光学性质。我们定义$|f(v)|=1$、$f(v)$连续且不可导的自发破缺点为极值破缺点，由数值结果可得，在极值破缺点位置处，系统会产生更加奇异的超强透反射率，所以本文主要研究极值破缺点附近的光传输性质。
波导长度为整数配比的情况有无数种，简单起见，作为最小奇数和最小偶数配比的代表，我们分别研究了$t=1,2$的情况，结果如下图所示。当$t=1$时，出现一个极值破缺点，其$n_I=1.32\times10^{-8}$。当$t=2$时，出现三个个极值破缺点，其$n_I$分别为$1.02\times10^{-6},1.25\times10^{-8},1.34\times10^{-6}$。


下一节，我们通过这些极值破缺点的高度值确定光波导网络的结构参数，然后，计算出在极值破缺点频率附近网络产生的奇异的超强的透反射率。

整数配比网络的奇异透反射率

通过研究，我们发现在PT对称光波导网络中，处于红黄交界的极值破缺点附近区域会出现奇异的透反射率，而且当元胞的数目为1时透反射率能达到最大值。我们给出了具有一个元胞、波导长度配比$d_1:d_2$分别为$1:1,1:2$整数配比的1D PTSTSCTOWNs在极值破缺点附近产生的透反射率，如下图所示，$T_L,T_R,R_L,R_R$分别代表左入射透射率、右入射透射率、左入射反射率以及右入射反射率。

从图像可知，1D PTSTSCTOWNs表现出超强的透反射率以及类似于光子禁带中超强的衰减特性，显然，该网络在设计高效光子储能器、高功率的超发光二极管和滤波器、高效光学滤波器等全光器件方面具有潜在的应用价值。此外，左入射和右入射的透反射谱的曲线都不重合，表明PT对称光学系统特有的、EM传播左右不对易性。
对于PT对称光波导网络为什么能产生超强的透反射率？本研究组也作出了详细的解释。能够产生这种超强的奇异透反射率，正是因为每条光波导中的增益材料和损耗材料形成了耦合谐振腔。PT对称网络中的增益和损耗材料不仅不会互相抵消、互相减弱光子的增益或损耗效应，而且会相互耦合，互相促进光子的增益和损耗效应。并且，在自发破缺点附近，APM和GPM边界的光子形成更加强烈的耦合共振效应，从而形成了尖锐的透反射峰和透射谷。

整数破缺配比网络的奇异透反射率

由上节我们可以知道在波导长度为整数配比时，1D PTSTSCTOWNs能产生超强的透射率，那么波导长度为整数破缺配比的网络也是否同样具备这种性质？本节将对波导长度为整数破缺配比网络的性质进行讨论与分析。为了得到极窄的光子频带，从而得到更加奇异的透反射率，我们进一步地减小了波导长度配比的整数破缺程度，计算了具有一个元胞、波导长度配比$d_1:d_2$分别为 $1:1-10^{-8},1:2-10^{-8}$的1D PTSTSCTOWNs在极值破缺点处产生的透反射率，其$n_I$分别为$1.35\times10^{-8},1.26\times10^{-8}$，结果如下图所示。

从图像可知，波导长度为整数破缺配比的网络也同样具备超强的透反射率以及超强的衰减的性质，而且还存在波导长度整数配比网络所没有的反射谷。该网络左右入射都存在反射谷，且反射谷所在频率的透射率大约为1，说明这种网络具备双向不可见的特性，可对隐形衣的设计提供理论依据。

结论

本文采用常见的二氧化硅材料设计了有趣的1D PTSTSCTOWNs，并且研究了EM在网络中的光学性质。
我们利用本研究组对光子模式重新划分为WPM和SPM的方法，对网络长度配比为整数和整数破缺的1D PTSTSCTOWNs的光子模式进行研究，寻找其新定义PT对称光学系统的极值破缺点，并且计算极值破缺点附近光子的透反射率。
我们的研究发现:(i)无论波导长度是整数配比还是整数破缺配比，网络都存在极值破缺点。当波导长度配比由整数到整数破缺时，有的极值破缺点会消失，有的极值破缺点频率位置会发生偏移，高度也会发生变化；(ii)波导长度为整数配比的1D PTSTSCTOWNs的透射率最大可达$10^{14}$数量级，反射率最大可达$10^{13}$数量级，拥有超强的奇异透反射率，这些性质对设计出高效光子储能器、高功率的超发光二极管等等全光器件具有重要的意义；(iii) 波导长度为整数破缺配比的1D PTSTSCTOWNs不仅具有超强的透反射率，还具有极深的反射谷。其透反射率最大可达$10^{13}$，反射谷的深度可达$10^{-13}$。该网络不仅能用于高效光子储能器、高功率的超发光二极管的设计，而且其双向不见的特性还能用于隐形衣的设计，还能够加深人们对PT对称光波导网络的认识和理解。

鸣谢

本篇博文精选自我的毕业论文，也非常幸运可以以共同第一作者发表在Chin.Phys.B上，在这里要感谢杨湘波教授、吴嘉野师兄和郑健师兄的指导，李海盈、林楷彬和郑宏挺同学的帮助。
PT对称光波导网络是我第一个进入科研领域的项目，也许也是最后一个，这段科研经历给我带来不少的精神财富。目前我已经本科毕业，每天老老实实上班，应该不会再有机会做这些前沿的光学领域的研究，也不会再有机会发表SCI论文了。你问我后悔吗？为什么不再去读个研究生？如果再给你一次机会，你是找工作还是读研究生？我的回答是不后悔，因为我感觉我自己的路并不那儿，至于研究生嘛，暂时是不会想了，也许我退休了，可以考虑一下！