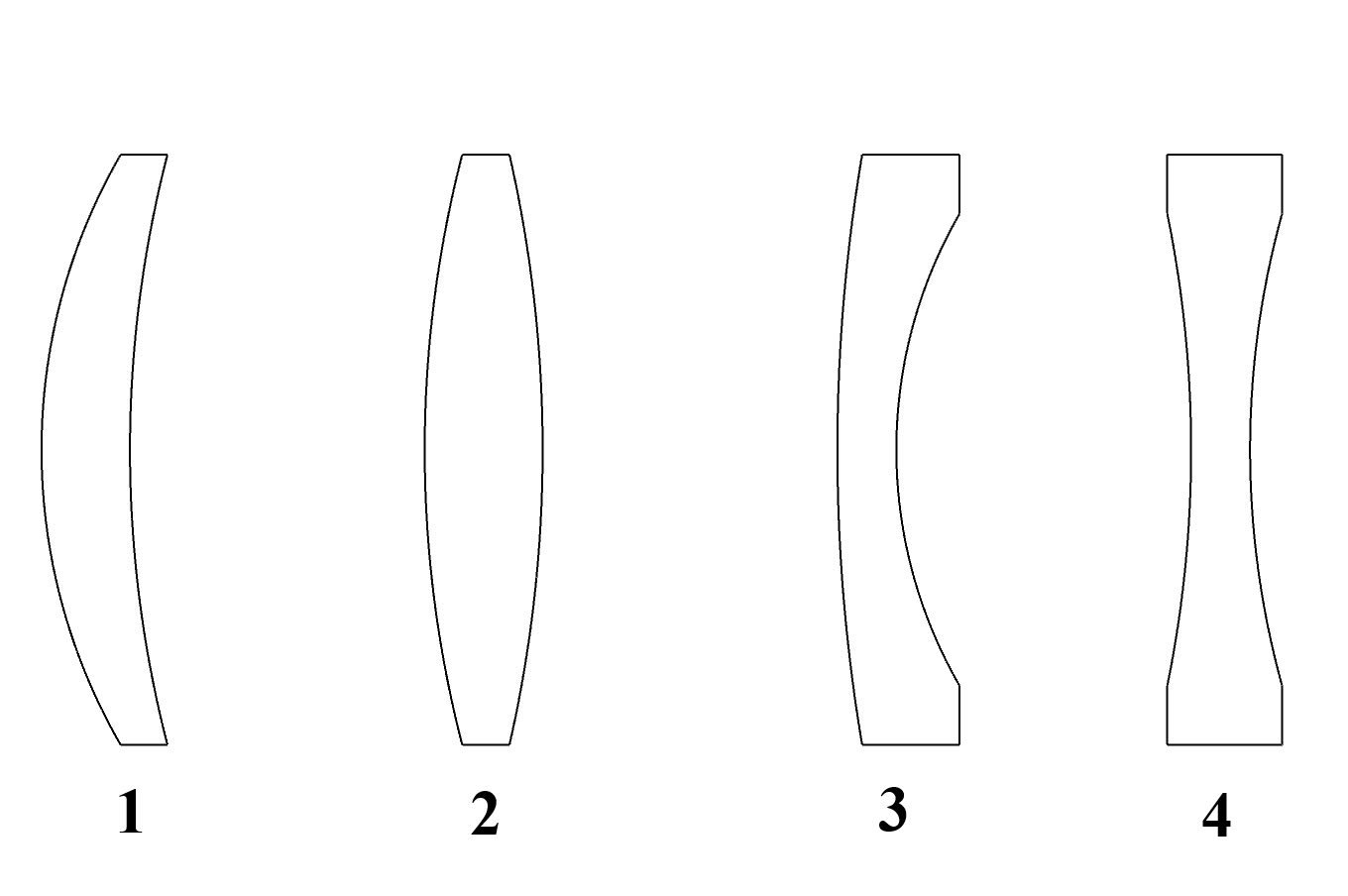
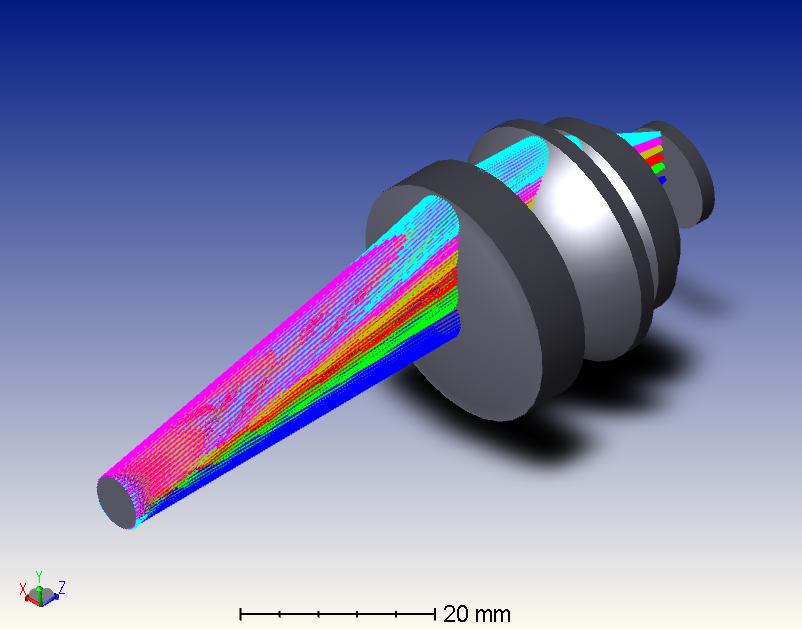
刃边法检测MTF程序设计(一)

引言

调制传递函数(Modulation Transfer Function)，简称MTF，是衡量镜头成像优劣的重要指标，有多种检测方法，如点光源法、狭缝法以及刃边法等。本文通过研究已知倾斜角度的理想刃边图像，简单介绍刃边法检测MTF的步骤及程序设计。

刃边法检测MTF步骤

1)读取倾斜角度为8度的理想刃边图像，得到二维矩阵Image;

2)选用二维高斯函数作为退化函数，与矩阵Image作卷积，人工模糊理想刃边图像，如下图所示;
该步骤仅用于理论验证刃边法检测MTF的可行性，实际检测过程不需要此步骤。

3)几何投影法将二维矩阵Image投影到一维，得到边缘拓展函数(Edeg Spread Function,简称ESF)，如下图所示;
以平行于刃边方向为$y$轴(物理含义为图像灰度值)，以垂直于刃边方向为$x$轴(物理含义为像素点投影后位置)。在程序中，设置嵌套循环，先投影第一列像素点位置，再投影第二列，如此类推，像素点投影到$x$轴关系如下$x=i\cdot cos\theta+j\cdot sin\theta$($\theta$为刃边倾斜角度)。
在检测刃边图像时，若直接提取$n\times n$个散点，会引入大量的噪声，经过求导后，噪声放大，最终会影响MTF检测的准确性。为了降低噪声的影响，增加测量结果信噪比，本次理论研究以1个像素为间隔求投影落点的灰度平均值。在检测实际刃边图像时，可以再缩小划分间隔，增加采样数量，但是还是会引入噪声，为了进一步降低噪声的影响，可用费米函数对边缘拓展函数进行拟合。本文仅进行理论验证，函数拟合暂时不详细展开。

4)边缘拓展函数求导得到线拓展函数(Line Spread Function,简称LSF)，如下图所示;

5)线拓展函数离散傅里叶变换得到MTF，如下图所示。
离散傅里叶变换定义如下$MTF=\sum_{i=0}^{N-1}LSF(n)\cdot exp(-\frac{2\pi nk}{N}j)$，若按照定义循环求和，程序的运算时间较长，增长检测工时，不利于工业化大批量生产，此处可以调整为行向量$LSF$与列向量$exp’$相乘，矩阵相乘后的结果取模归一化后得到MTF曲线。图像纵坐标代表MTF，该值经过归一化，无单位，横坐标代表空间频率，单位为周期/像素(cycles/pixel)。在实际检测中，横坐标的频率一般为线对(lp/mm或cycles/mm)，两者含义相同。若将单位周期/像素转换为线对，需要知道检测所用相机传感器的像素大小，例如，相机的像素大小为0.01mm，即100pixel=1mm，那么1cycles/pixel=100lp/mm。

程序设计

%%ESF2MTF.M%%
clc; clear all; close all;

Image=im2double(rgb2gray(imread('0.bmp'))); %获取图像矩阵

x=-5:0.01:5;
y=-5:0.01:5; 
sigma=0.1;
Point_Spr_Function=exp(-(x.^2+y.^2)/(2*sigma)^2); %高斯函数，起模糊作用

Image=conv2(Image,Point_Spr_Function,'same'); %将获取的矩阵与点扩散函数做卷积
subplot(2,2,1)
imshow(Image) %展示模糊后刃边
axis on

ESF_Size=floor(max(size(Image))*(cos(2*pi/45)+sin(2*pi/45)));
Edge_Spr_Function(1,ESF_Size)=0; %初始化参数

for w=1:size(Image)
    for h=1:size(Image)
        Space_X=(w*cos(2*pi/45)+h*sin(2*pi/45)); %几何投影
        Edge_Spr_Function(floor(Space_X))=(Edge_Spr_Function(floor(Space_X))+Image(h,w))/2;
    end
end

Edge_Spr_Function=Edge_Spr_Function(:,floor(0.25*ESF_Size):floor(0.75*ESF_Size)); %取刃边附近的灰度值
subplot(2,2,2)
Space_X=1:1:max(size(Edge_Spr_Function));
plot(Space_X,Edge_Spr_Function,'k.')  %几何投影法将矩阵投影到一维数轴，获取边缘扩散函数

Space_X=Space_X(:,1:(max(size(Space_X)-1)));
Linear_Spr_Function=diff(Edge_Spr_Function); %矩阵方式求导
subplot(2,2,3)
plot(Space_X,Linear_Spr_Function,'k.') %离散点求导得到线扩散函数

Max_Fre=5;
omega=0:0.1:Max_Fre; %初始化参数

Num=1:(max(size(Space_X)));
Modul_Tran_Function=Linear_Spr_Function*exp(-i*(2*pi/(max(size(Space_X)))).*Num'*omega);
Modul_Tran_Function=abs(Modul_Tran_Function);
Modul_Tran_Function=Modul_Tran_Function./Modul_Tran_Function(1); %线扩散函数离散点作非周期傅里叶变换，得到MTF
subplot(2,2,4)
plot(omega,Modul_Tran_Function)
axis([0 Max_Fre 0 1])